Função e equação de 2º grau

As funções de 2º grau são importantes ferramentas para cálculos em diversos campos da física
A parábola é uma cônica, mesma família das circunferências, elipses e hipérboles. Uma parábola é formada pelos pontos que mantêm a mesma distância de um ponto F (foco) e uma reta r (diretriz).
Veja na figura abaixo que, para qualquer ponto da parábola (P, P’ e P’’), a distância até F é igual à distância até r.
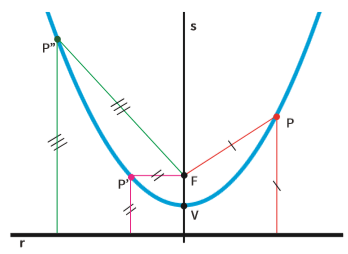
- → O ponto F é o foco da parábola
- → A reta r é a diretriz
- → O ponto V é o vértice
- → Passando pelo vértice e pelo foco, perpendicularmente à diretriz, está a reta s, que é o eixo de simetria da parábola
Pontos notáveis da parábola
Normalmente, trabalhamos com as parábolas no plano cartesiano, ou seja, sobre os eixos x e y. No plano, é possível localizar os chamados pontos notáveis da parábola:
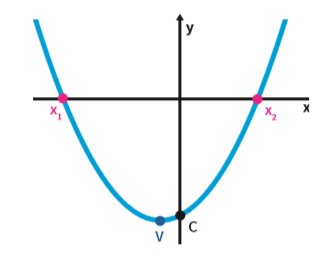
- → V é o vértice.
- → Os pontos x1 e x2 são as chamadas raízes da parábola – os pontos nos quais a curva corta o eixo x.
- → O ponto C é a intersecção da parábola com o eixo y.
As equações de uma parábola
Toda parábola é definida por uma função de 2º grau. Esse tipo de função pode ser apresentado de três formas distintas.
1) Forma geral: y = a . x2 + b . x + c
É a forma mais conhecida. Observe nos gráficos a seguir como é possível deduzir uma série de informações sobre a parábola, só analisando a função que a define:
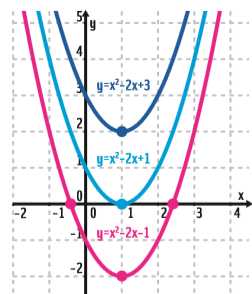
Observe que:
- → As três parábolas têm a concavidade voltada para cima.
- → Em todas as funções, o coeficiente a = 1. Ou seja, o termo x2 é multiplicado por 1.
- → A parábola azul-escura não tem raiz (a curva não cruza o eixo x); a azul-clara tem uma única raiz, que coincide com o vértice V; a rosa tem duas raízes.
- → Nas três funções, o valor do coeficiente c coincide com o ponto em que a curva corta o eixo y
Agora observe os gráficos de outras três parábolas:
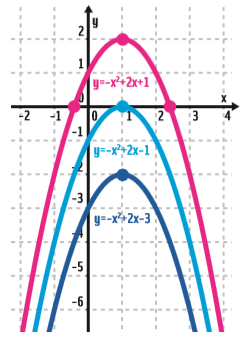
Veja que:
- → As três têm a concavidade voltada para baixo.
- → Todas as funções têm o coeficiente a = – 1.
- → A parábola azul-escura não tem raízes, a azul-clara, tem uma única raiz, e a rosa tem duas raízes.
- → Cada uma das parábolas cruza o eixo y no ponto que corresponde ao valor de c na função.
Da comparação entre os dois conjuntos de parábolas, podemos concluir que:
- → O parâmetro a está relacionado à concavidade da parábola:
- → Se a > 0, a concavidade é para cima;
- → Se a < 0, a concavidade é para baixo.
- → O parâmetro c é exatamente o valor da coordenada y do ponto em que a parábola corta o eixo y (no ponto em que x = 0).
- → O número de raízes está relacionado com o número de pontos em que a parábola cruza o eixo x.
- → Quando a concavidade da parábola é voltada para cima, dizemos que o vértice é o ponto de mínimo, ou seja, o vértice é o ponto da parábola no qual a coordenada y tem o menor valor possível. Da mesma maneira, se a parábola tem concavidade para baixo, chamamos o vértice de ponto de máximo – aquele em que a coordenada y atinge o maior valor possível.
2) Forma fatorada: y = a . (x – x1) . (x – x2)
Neste caso, x1 e x2 são as raízes da função – ou seja, os valores de x para os quais y = 0.
É claro que só se pode representar uma parábola com a função na forma fatorada se ela tiver raízes.
Desenvolvendo a forma fatorada:
- y = a . (x – x1) . (x – x2)
- y = a . (x2 – x . x1 – x . x2 + x1 . x2)
- y = a . (x2 – x . (x1 + x2) + x1 . x2)
Vamos considerar que:
- x1 + x2 = S, ou seja, S é a soma das raízes.
- x1 . x2 = P, ou seja, P é o produto das raízes.
Substituindo S e P na última etapa do desenvolvimento da função acima, temos:
- y = a . (x2 – x . S + P)
- y = a . x2 – a . S . x + a . P
Comparando essa função com a forma geral:
![]()
![]()
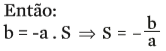
![]()
Isso significa que os coeficientes da forma geral têm relação direta com as raízes da função.
3) Forma canônica: y = a . (x – x v )2 + y v
Esta forma descreve a parábola a partir das coordenadas de seu vértice V – ou seja, das coordenadas (xv , yv) – e de mais um ponto. O parâmetro a, novamente, é a concavidade da parábola.
A forma canônica é muito útil na solução de problemas em que as coordenadas do vértice são conhecidas.
Fórmula de Bhaskara
É a fórmula que determina as raízes de uma função de 2º grau, se elas existirem. A fórmula de Bhaskara é utilizada para resolver a equação da parábola na forma geral:
a . x2 + b . x + c = 0
Para isso, basta substituir os coeficientes a, b e c na fórmula:
![]()
O radicando de ![]() é chamado de discriminante, ou delta (∆):
é chamado de discriminante, ou delta (∆):
= b2 – 4 . a . c
A fórmula ficaria, então:
![]()
A equação terá:
- → duas soluções se ∆ > 0
- → uma solução se ∆ = 0
- → ou nenhuma solução se ∆ < 0
As coordenadas do vértice
Quando temos a função de 2º grau em sua forma geral, podemos obter as coordenadas do vértice aproveitando o fato de que toda parábola é simétrica. Observe:
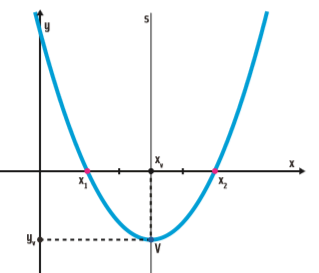 O eixo s é o eixo de simetria.
O eixo s é o eixo de simetria.
Repare que a coordenada x do vértice V está bem no meio do segmento que une as raízes x1 e x2: xv é o ponto médio desse segmento. Então, o valor da coordenada x do vértice V é a média aritmética das coordenadas x das raízes.
Por Bhaskara, sabemos que as duas raízes são:
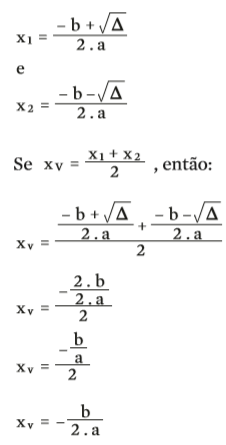
Se substituirmos esse valor na forma geral da função de 2º grau, obtermos yv:
![]()

CANÔNICA E GERAL
Obtenha a forma geral da função quadrática representada no gráfico abaixo:
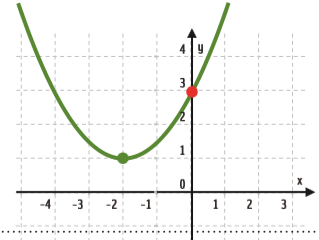
Do gráfico obtemos as coordenadas do vértice (V) e do ponto (P) no qual a curva intersecta o eixo y: V(-2, 1) e P(0, 3). Substituindo as coordenadas de V na forma canônica da função, temos:
![]()
Substituindo as coordenadas de P, ficamos com
![]()
Vamos substituir o valor encontrado para a na expressão (I):
![]()
Esta é a equação na forma geral.

FORMA FATORADA
As raízes da função f(x) = ax² + bx + c são x1 = 3 e x2 = 5. O vértice da parábola de f(x) tem coordenadas (4,1). Em que ponto o gráfico dessa função cruza o eixo das ordenadas?
- → No ponto em que a parábola de f(x) cruza o eixo y, x = 0;
- → Substituindo x = 0 na forma geral da função, obtemos y = c;
- → O enunciado fornece as duas raízes da função, que podem entrar na forma fatorada da função. Então,
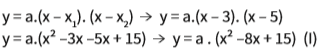
Para calcular o valor de a, basta substituir as coordenadas do vértice: (4, 1):
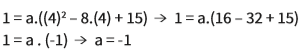
Substituindo esse valor na expressão (I), obtemos:
![]()
O gráfico da função cruza o eixo y no ponto (0, -15).
COORDENADAS DO VÉRTICE
Determine as coordenadas do vértice da função quadrática que passa pelos pontos P(0, -2) e Q(3, 4), sabendo que uma de suas raízes é x = – 1.
Primeiro, vamos obter a expressão da forma geral da função. Depois, calcular as coordenadas do vértice a partir dos coeficientes a, b e c.
Repare que conhecemos três pontos da parábola: P (0, -2), Q (3,4) e o ponto correspondente à raiz. Raiz, você se lembra, é o ponto em que a parábola corta o eixo x. E nesse ponto, y sempre vale zero. Então, conhecemos um ponto R (-1, 0).
A forma geral da função de 2º grau é y = ax² + bx + c. Substituindo cada um desses pontos nessa forma geral, ficamos com três equações:
Para o ponto P (0, -2), temos a equação (I):
![]()
Para o ponto Q (3,4), temos a equação (II). Aqui já substituímos o valor de c = -2. Veja como fica:
![]()
Por fim, para o ponto R (-1, 0), definirmos a equação (III)
![]()
Com as equações (II) e (III) montamos um sistema de equações:
![]()
Multiplicamos a equação (III) por 3. Ficamos com:
![]()
Agora, somamos as equações:
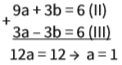
Substituindo o valor de a em (II), obtemos:
![]()
Se encontramos os coeficientes a = 1 e b = – 1, temos a forma geral da função da parábola:
![]()
Para encontrar a coordenada x do vértice V(X,Y) , usamos a fórmula:
![]()
Substituindo o valor de xv na função, em sua forma geral, encontraremos a coordenada yv:
![]()
Portanto, o vértice tem coordenadas V (1/2, –9/4).
Máximo e mínimo
Nas funções em que a < 0, a parábola tem concavidade voltada para baixo. Com isso, o vértice é o ponto mais alto da curva – ou seja, sua coordenada y é maior que a de qualquer outro ponto da parábola. Nesse caso, o vértice é chamado de ponto de máximo da função.
Já se a função tem a > 0, a parábola tem con- cavidade voltada para cima. O vértice é o ponto mais baixo da curva, e sua coordenada y, a menor de todos os pontos quer a formam. Nesse caso, o vértice é chamado de ponto de mínimo da função.
Os pontos máximos e mínimos das parábolas têm aplicações muito práticas.
PONTO MAXÍMO
Um fazendeiro deseja cercar uma área retangular para fazer um galinheiro. Ele dispõe de 16 metros de alambrado. E um dos lados do galinheiro não precisa da cerca porque é um muro. Qual é a maior área possível desse galinheiro?
A figura abaixo mostra a situação do enunciado:
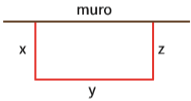
O alambrado será usado para fechar apenas três lados do retângulo, ou seja, os 16 metros de alambrado irá cobrir dois comprimentos x (altura do retângulo) e um comprimento y (largura).
Então: 2x + y = 16 y = 16 – 2x (I)
A área do galinheiro é a área do retângulo: A = x . y Substituindo o valor de y encontrado em (I) na expressão da área, obtemos:
A = x . (16 – 2x) • A = 16x – 2x²
Esta é uma função de 2º grau, com coeficiente a = -2. O coeficiente é negativo, então a parábola tem concavidade voltada para baixo. E seu vértice será o ponto máximo – o ponto que corresponde à área máxima possível para o retângulo. Calculando o valor de x no vértice:
xV = – b / 2a
Portanto, a área do galinheiro é máxima quando os lados x medem 4 metros.
Com dois lados medindo 4 metros, para cobrir a altu- ra do retângulo o fazendeiro consumirá 8 metros do alambrado disponível. Os restantes 8 metros cobrem o terceiro lado (largura).
Então a área do retângulo é A = 8 . 4 = 32 m2

COMO É CONSTRUÍDO O M DO MCDONALD’S
Os designers gráficos empregam várias figuras geométricas no desenho de logotipos. Observe com atenção o logo da rede de lanchonetes McDonald’s. Repare que as pernas da letra M têm a forma muito parecida com a de duas parábolas:

O M no plano cartesiano:
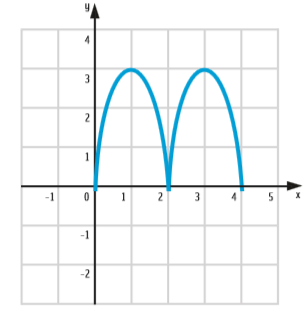
Trabalhando apenas com metade do logotipo, podemos reconhecer os pontos notáveis da parábola da esquerda: o vértice Ve e as raízes x1 e x2 da função de 2º grau que define a parábola:
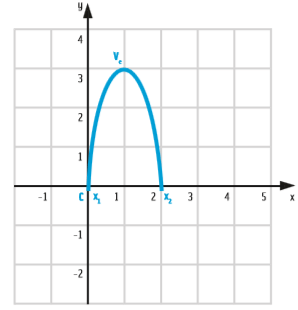
- → O vértice tem as coordenadas V (1, 3).
- → O ponto x1 tem como coordenadas (0, 0).
- → O ponto x2 tem como coordenadas (2, 0).
Repare:
- → A concavidade é voltada para baixo. Isso significa que o coeficiente a deve ser negativo.
- → A parábola corta o eixo y no ponto zero. Então o coeficiente c deve ser nulo.
Podemos, agora, deduzir a função que define cada um dos pontos da figura, por dois caminhos:
1) A partir das coordenadas do vértice (V)
Vamos trabalhar com a forma canônica da função. Para isso, devemos conhecer as coordenadas do vértice e as de mais um ponto da parábola – o ponto x2, por exemplo. Então, temos estes dados:
![]()
Substituindo as coordenadas do vértice em
![]()
![]()
Desenvolvendo:
![]()
Para obter o valor do coeficiente a, substitui- mos as coordenadas do outro ponto conhecido, x2 = (2, 0). Ou seja, x = 2 e y = 0.
Então:
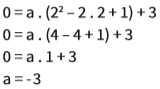
Substituindo esse valor em (I), temos:
![]()
Aplicando a propriedade distributiva da multiplicação, obtemos:
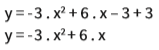
Está confirmado: o coeficiente a é negativo e o coeficiente c é nulo.
2) A partir das raízes
Se conhecemos as raízes de uma função de 2º grau, conseguimos obter a expressão da função em sua forma
geral a partir da forma fatorada. Vamos aplicar essa estratégia para obter a função da parábola da direita do logotipo do McDonald’s:
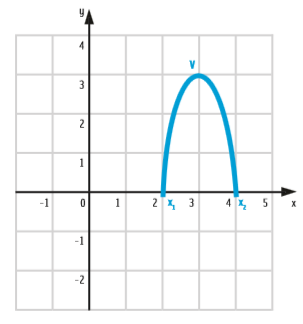
Só de observar a figura já sabemos que:
- → As raízes da função que define essa parábola são:
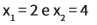
- O vértice tem como coordenadas Vd (3, 3)
Vamos substituir as raízes na forma fatorada da função:
![]()
Efetuando a multiplicação indicada, temos:
![]()
Agora, é só substituir as coordenadas do outro ponto conhecido, no caso o vértice V (3, 3):
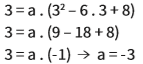
Essa é a forma geral da função de 2º grau que tem como gráfico a parábola da direita do logotipo do McDonald’s.
Observe que, assim como na primeira parábola, o coeficiente a desta segunda parábola também é negativo: sua concavidade é para baixo. E tem o mesmo valor (-3).
Os outros coeficientes (b e c) também influem na localização de cada parábola no plano cartesiano. No caso da parábola da direita, c = -24 significa que, se a parábola fosse prolongada, ela cruzaria o eixo y na coordenada (0, -24).




















