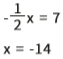Potência e Logaritmo: Funções e equações exponenciais

As expressões para variações muito grandes

Como resolver funções em que a variável é o expoente de um número

Função exponencial é aquela que tem como  variável independente o expoente de uma potência. Ou seja, a variável dependente é definida em função de uma potência. Funções exponenciais têm a seguinte forma geral:
f(x) = m . a^x, em que:
• f(x) é a variável dependente;
• x é a variável independente;
• m é um número real qualquer;
• a é um número real maior que zero e diferente de 1.

As  funções exponenciais são usadas em diversas situações da economia e das ciências – no cálculo de juros compostos, na estimativa de crescimento de uma população ou na redução da amostra de um elemento radioativo, que variam em progressão geométrica.

FUNÇÕES CRESCENTES

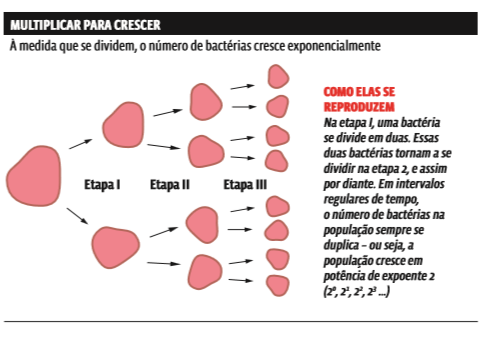
As funções exponenciais podem ser crescentes ou decrescentes. Exemplo de função crescente é a que descreve o crescimento de uma população de bactérias – microrganismos que se reproduzem por simples divisão celular. A multiplicação de bactérias segue uma regularidade: a partir da população inicial, é possível calcular o tamanho da população depois de determinado tempo.

Bactérias –  O QUE ISSO TEM A VER COM A BIOLOGIA?
As bactérias são microrganismos unicelulares, que se reproduzem por mitose – cada célula se divide em duas, que carregam material genético idêntico.

Imagine que um tipo de bactéria se divida a cada 3 horas. Vamos chamar de x a quantidade de períodos de 3 horas, e de y o número de bactérias a cada etapa. Se partimos de uma única bactéria, a tabela é a seguinte: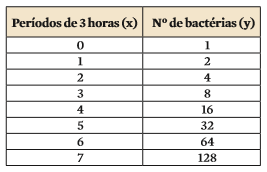
Repare que o número de bactérias se duplica a cada etapa. Então y varia em função de uma potência de base 2.
A função que descreve o número de bactérias ao longo do tempo é:
y = 1 . 2^x

Agora imagine que a população inicial seja de três bactérias. Cada uma se divide em duas, seguidamente. Então y continua variando em função de uma potência de base 2. Mas, como partimos de três bactérias, os valores são multiplicados por 3. A tabela ficaria assim:

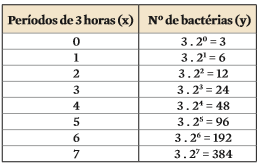
Generalizando, para uma população inicial de três bactérias, a função para a variação de y é:
y = 3 . 2^x

De modo geral, a função que descreve o crescimento das bactérias é:
y = m . 2^x , em que:
•  m é a quantidade inicial de bactérias, no momento zero (x = 0);
• 2 é a razão de crescimento.

Como o número de bactérias sempre aumenta, esta é uma função crescente.

FUNÇÕES CRESCENTES

O exemplo clássico de função exponencial decrescente é a desintegração radioativa.  Esse fenômeno ocorre naturalmente com os elementos químicos no final da tabela periódica, como urânio e o radônio.

A desintegração obedece à lei geral: em intervalos regulares de tempo, metade dos átomos de uma amostra se desintegra, transformando- se em elementos químicos mais leves. Cada um desses intervalos é chamado meia-vida.

Diferentes elementos se desintegram em diferentes períodos. O urânio-238 tem meia-vida de cerca de 4,5 bilhões de anos – ou seja, uma amostra de mil átomos de urânio-238 precisa de 4,5 bilhões de anos (praticamente a idade da Terra) para se reduzir à metade. Já para o radônio-220, bastam pouco mais de 50 segundos para isso acontecer.

O iodo-131, muito utilizado em exames de diagnóstico por imagem, também é um elemento radioativo. Quando o paciente passa por uma máquina de tomografa computadorizada, o iodo-131 denuncia a presença de um tumor.

Como todo elemento radioativo, o iodo-131 também tem seu período de meia-vida. Se injetarmos uma amostra de 100 gramas de iodo-131 em um paciente, oito dias depois restarão no organismo apenas 50 gramas do elemento ainda radioativo. Mais oito dias, e o material radioativo terá decaído pela metade, novamente: restarão apenas 25 gramas. E assim por diante.

Considerando que a massa de iodo radioativo seja y, e a quantidade de períodos de meia-vida seja a variável x, é possível montar uma tabela que indique o que resta de material radioativo no organismo do paciente depois de determinado tempo.

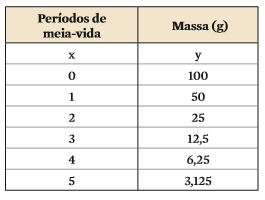
Repare que a sequência de valores para y é obtida pela divisão do valor anterior por dois. Ora, dividir por dois é a mesma coisa que multiplicar por ½. Isso significa que essa sequência é uma sucessão de multiplicações por ½. É aí que surge a potência, agora de base ½.

A função que descreve o fenômeno é, então:

Note que a forma geral dessa função é a mesma que a da função para a duplicação de bactérias. Entretanto, na primeira situação, a base da potência era 2, que é maior que 1. Isso indica que o y cresce conforme x cresce – função crescente.
Já no segundo caso, a base tem valor positivo, mas é uma fração, ou seja, menor que 1. Então, neste caso, à medida que x cresce, o valor de y cai – função decrescente.

GRÁFICOS DA FUNÇÃO EXPONENCIAL

Funções crescentes e decrescentes definem gráficos diferentes. Vamos retomar os exemplos da duplicação de bactérias e do decaimento de iodo-131 e analisar cada situação.

Duplicação das bactérias: função crescente →
y = a . 2^x

Decaimento radioativo: função decrescente →

Repare que a diferença fundamental entre as expressões das duas funções é o valor da base da potência:
• N a função crescente, trata-se de um valor maior que 1;
• Na função decrescente, a base da potência é um valor positivo, ou seja, maior que zero, porém menor que 1. É a lógica: dividir por dois é o mesmo que multiplicar por ½.

Decaimento – O QUE ISSO TEM A VER COM A QUÍMICA?
O decaimento radioativo ocorre em átomos de elementos químicos que têm um número exagerado de prótons. Prótons têm carga elétrica positiva, e quando existem prótons demais, a força de repulsão entre eles é tão intensa que os nêutrons não conseguem manter o núcleo inteiro. Este é um fenômeno físico. Mas, para a química, conhecer esse processo é importante para o desenvolvimento de substâncias como as usadas em diagnóstico por imagem.

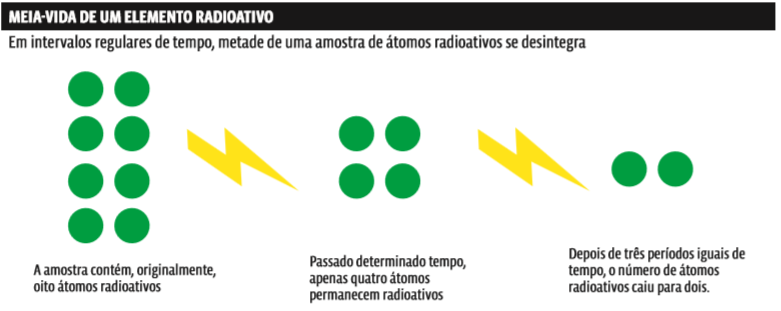
METADE DA METADE. O número de átomos de uma amostra radioativa cai pela metade a intervalos regulares de tempo. No infográfico você vê como essa queda ocorre. Da amostra original de 8 átomos radioativos, apenas 4, a metade, não se desintegraram em elementos mais leves, depois do intervalo de tempo t. Passado outro intervalo t, o número de átomos radioativos cai de novo pela metade: de 4 para 2. O decaimento obedece a uma função exponencial de base 1/2.

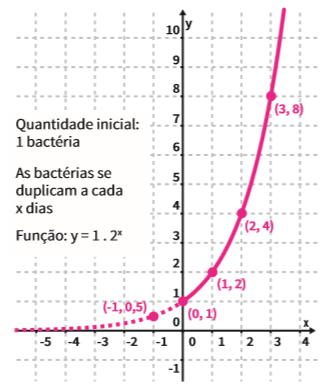
CRESCIMENTO DE BACTÉRIAS

CONCENTRAÇÃO DE IODO-131

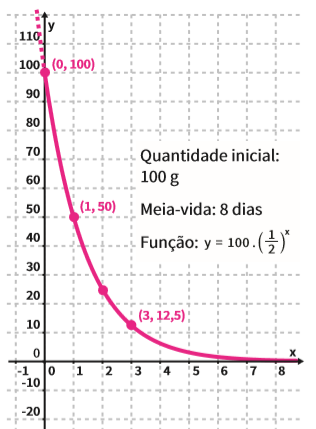
A respeito dos dois gráficos, podemos ressaltar:
• Ambas as curvas passam pelo ponto (0, m). No gráfico das bactérias, m = 1; no gráfico da concentração de iodo, m = 100. Isso ocorre quando o expoente x assume valor zero. E qualquer número elevado a zero é igual a 1. Veja:
y = m . a^x
y = m . a^o = m . 1
Então, y = m

• As curvas se aproximam do eixo x sem jamais tocá-lo, formando aquilo que em matemática se chama de assíntota: duas curvas que não são paralelas tendem a se aproximar mais e mais, mas nunca se tocam. Isso ocorre porque o valor de y nunca chegará a zero, pois a base da potência é sempre diferente de zero.
• O eixo x representa o tempo. A parte pontilhada no alto do gráfico da concentração de iodo 131 mostra como seria a curva se fosse possível contar o tempo antes do início (zero).

EQUAÇÃO EXPONENCIAL

São equações nas quais a incógnita é o expoente de uma potência. Se duas potências com bases iguais são iguais, então, seus expoentes também são iguais. Veja:

a^x = a^p → x = p.

A estratégia para resolver uma equação exponencial é usar as propriedades das potências para igualar as bases nos dois membros da equação. Acompanhe no exemplo a seguir:

Qual o valor do expoente x que torna verdadeira a equação?

Repare que tanto 9 quanto 27 podem ser reescritos como potências de base 3:

9 = 3² e 27 = 3³

Então podemos reescrever a equação:

Pela propriedade de potência de potência, eliminamos os parênteses no primeiro membro:

3^–2x = 3³

Numa igualdade entre potências, se as bases são iguais, os expoentes também devem ser iguais. Portanto:

EQUAÇÃO EXPONENCIAL

Resolva a equação 

A fração 1/2 pode ser escrita como 2^–1. E 128 é o mesmo que 2⁷

Então, podemos reescrever a equação assim:

Pela propriedade de expoentes fracionários, sabemos que    é o mesmo que 2^-1/2

Então podemos reescrever a equação, de novo:

Pela propriedade de potência de potência, multiplicamos os expoentes do 1º termo da expressão:

Temos agora duas potências de mesma base. Portanto, os expoentes também devem ser os mesmos: