Cinemática: MRU (Movimento Retilíneo Uniforme)

RAIO O jamaicano Usain Bolt corre 100 metros em 9,6 segundos. Nessa velocidade constante, ele percorreria 1 quilômetro em 1,5 minuto
Em linha reta e no mesmo ritmo
Corpos que se deslocam em trajetória retilínea e com velocidade constante – ou seja, sem aceleração – estão em movimento retilíneo uniforme, ou MRU. Corpos em MRU percorrem sempre a mesma distância em um mesmo intervalo de tempo.
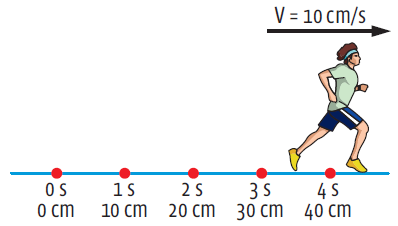
Função horária da posição
Para um corpo em MRU, a posição num instante t qualquer é dada pela função horária da posição:
S (t) = S0 + v . t, em que:
-> S0 é posição inicial, no instante t = 0;
-> v é a velocidade de deslocamento;
-> t é o tempo do deslocamento.
Conhecendo a posição inicial (S0) e a velocidade de deslocamento (v), podemos calcular a posição S(t) que o corpo ocupa em um instante qualquer (t). Com isso, determinamos o comportamento do objeto móvel no decorrer do tempo.
No S.I., a posição dos corpos é medida em metros e a velocidade, em m/s. Lembre-se de que, em movimentos progressivos, os corpos apresentam velocidade positiva e, em movimentos retrógrados, velocidade negativa.
Repare que a expressão S (t) = S0 + v . t é uma função do 1° grau. Seu coeficiente linear determina a posição inicial S0 do corpo e o coeficiente angular, a velocidade v do corpo.
Gráficos do MRU
É muito comum na cinemática o estudo do movimento de um corpo ser feito por meio de gráficos que relacionam os parâmetros físicos do movimento com o tempo. A equação que define um MRU é uma função linear (ou função de 1º grau), e, por isso, sempre determina uma reta.
Velocidade em função do tempo
Todo corpo que executa MRU mantém uma velocidade constante. Se a intensidade da velocidade não varia, então o gráfico da velocidade em função do tempo deve ser uma reta paralela ao eixo do tempo.
No caso de um corpo móvel que executa um movimento progressivo (no sentido adotado como positivo), a velocidade é positiva. Assim, o gráfico da velocidade em função do tempo é uma reta acima da velocidade v = 0. Veja:
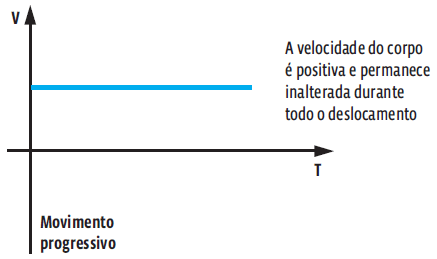
Já um objeto em um MRU retrógrado, a velocidade é negativa. Para essa situação, o gráfico da velocidade em função do tempo também é uma reta, mas na posição em que v < 0. Veja:
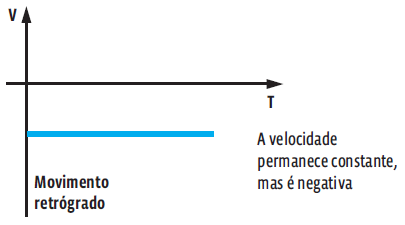
A área sob a curva do gráfico é numericamente igual ao deslocamento escalar sofrido pelo corpo nesse intervalo de tempo. Veja:
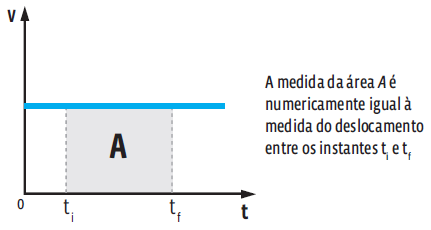
Mas atenção: a área, naturalmente, não indica o sentido do deslocamento. Para definirmos se o deslocamento é positivo ou negativo, devemos analisar se o movimento é progressivo (ΔS > 0) ou retrógrado (ΔS < 0).
Posição em função do tempo
Podemos também construir gráficos que representem a posição de um corpo que executa MRU em cada instante do percurso. Para isso, basta construir o gráfico da mesma função horária da posição:
S (t) = S0 + v . t
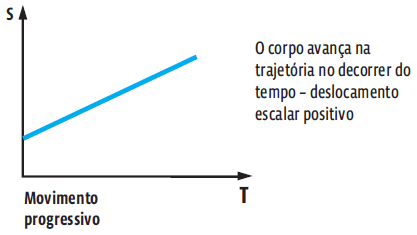
Num movimento progressivo (v > 0), o móvel avança nas posições ao longo da trajetória com o passar do tempo, a partir de um ponto de origem. Assim, o gráfico da posição em função do tempo é uma reta crescente.
![]()
Função de 1º grau é aquela na qual uma variável (y) depende de outra variável (x), que é independente e é elevada à primeira potência:
![]()
Note que a é o coeficiente angular da reta, e é definido pela diferença entre as coordenadas x e y de dois pontos quaisquer da reta:
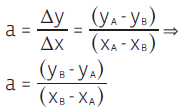
E b é o coeficiente linear da reta: o valor de y no ponto em que a reta cruza o eixo y (ou seja,o ponto que tem a coordenada x = 0).
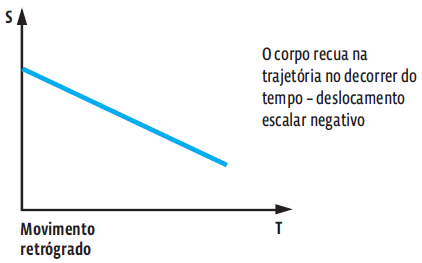
No caso de um movimento retrógrado (v < 0),o móvel recua a partir de um ponto de origem.Então, o gráfico é uma reta decrescente. Veja:
Acompanhe o raciocínio: um automóvel percorre uma trajetória retilínea. Sua posição em função do tempo é representada no gráfico:
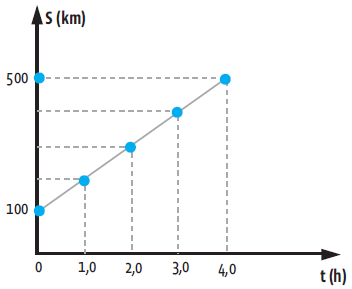
• A posição inicial do automóvel é 100 km (para t = 0 h, S0 = 100 km);
• A posição final do automóvel é 500 km (para t = 4 h, Sf = 500 km);
• O gráfico é uma reta, então trata-se de um movimento uniforme;
• O movimento é progressivo porque a reta é ascendente.
A velocidade média do automóvel é a razão entre o deslocamento escalar e o tempo de percurso:
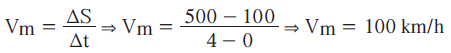
Repare que, num gráfco da posição em função do tempo para um corpo em MRU, a velocidade é o coeficiente angular da reta.
Para construir a função horária da posição do automóvel em determinado intervalo, basta substituir os valores conhecidos (S0 e v):
![]()
Esta é a função específica para o movimento desse automóvel. Então, podemos calcular sua posição em qualquer momento da viagem. Veja:
Qual a posição do automóvel depois de 2,5 horas de viagem?
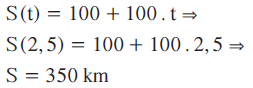
Encontro de dois corpos
O encontro de dois objetos que se movem sempre se dá no momento em que eles ocupam a mesma posição na trajetória.
Dois corpos seguem uma mesma trajetória retilínea movendo-se em sentidos opostos, com velocidade constante. Veja abaixo:
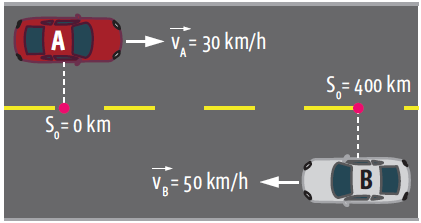
Os dois veículos, é claro, vão se encontrar na mesma posição. Matematicamente, temos: SA= SB.
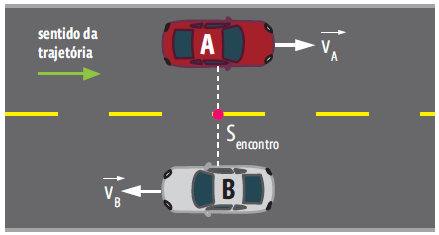
Conhecemos as posições iniciais e as velocidades de A e B. Adotando que o sentido positivo da trajetória é da esquerda para a direita, e substituindo esses valores na função horária, temos:
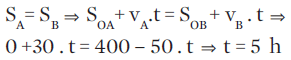
Portanto, os automóveis irão se encontrar após cinco horas.
Para definir a posição em que eles se encontrarão, é só substituir os valores conhecidos na equação horária de qualquer um dos veículos:








