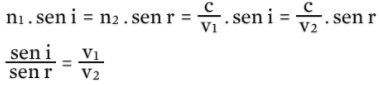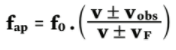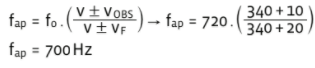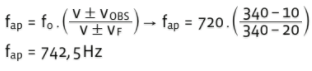Ondulatória: Fenômenos


Dois dos fenômenos ondulatórios clássicos são a refração e a reflexão – temas que você vê na óptica (tema do capítulo 4). As leis e propriedades que explicam a refração e a reflexão da luz valem para qualquer tipo de onda.
Reflexão é o que acontece quando uma onda, ao se propagar, encontra um obstáculo e retorna – como no eco. Como para as ondas de luz, o ângulo de incidência de qualquer onda é igual ao ângulo de reflexão, para o mesmo meio de propagação. Os valores do módulo da velocidade, da frequência e do comprimento de onda refletida também são iguais aos da onda incidente.
Refração ocorre quando a onda muda de meio – por exemplo, o som que vem pelo ar e encontra a água. A relação entre os ângulos de incidência e refração de uma onda com sua velocidade e comprimento de onda é derivada da definição de índice de refração de um material e da lei de Snell, utilizada para a refração da luz. Recordando:
Para a luz, o índice de refração absoluto de um material é a relação entre a velocidade no vácuo (c) e velocidade no material: n = c/v, em que:
• n é o índice de refração do material que é atravessado pela luz;
• c é a velocidade da luz no vácuo;
• v é a velocidade da luz no material que ela atravessa.
A relação entre os ângulos de incidência e refração é dada pela lei de Snell:
n1. sen i = n2 . sen r, em que
• n1 é o índice de refração do material 1;
• n2, o índice de refração do material 2;
• i é o ângulo de incidência;
• r é o ângulo de refração.
Os ângulos de incidência (i) e de refração (r) são medidos em relação à reta normal, perpendicular à superfície de separação entre os dois meios.
Para a luz, substituindo n, temos:
Para ondas em geral, sabemos que v = λ . f
A frequência da onda se mantém na troca de meio. Portanto,

InterferênciaQuando duas ou mais ondas se sobrepõem, uma interfere sobre a outra. Isso acontece, por exemplo, quando lançamos mais de uma pedra num lago. O estudo da interferência de ondas é complexo quando se trata de ondas com características diferentes. Vamos nos deter no caso mais simples, no qual as ondas que se superpõem são idênticas, ou seja, têm a mesma frequência e o mesmo comprimento de onda.
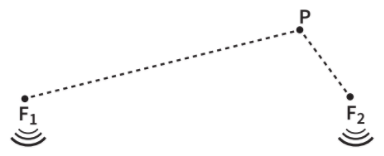
A figura abaixo representa dois alto-falantes instalados em dois pontos diferentes de uma sala (F1 e F2), que emitem ondas idênticas.
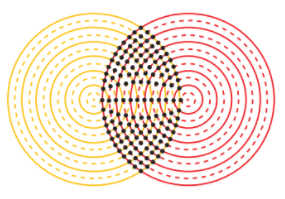
Em alguns lugares, entre F1 , F2 e P, a intensidade do som será mais intensa, e, em outros, não será possível ouvir nada. Nos pontos nos quais a intensidade sonora é reforçada ocorre interferência construtiva; naqueles em que a intensidade é nula temos uma interferência destrutiva. Veja na ilustração abaixo:
As linhas cheias correspondem a cristas da onda. E cada linha tracejada, a vales da onda. Nos pontos onde os vales se encontram
![]() ocorre interferência destrutiva. Já naqueles em que as cristas se encontram, interferência construtiva
ocorre interferência destrutiva. Já naqueles em que as cristas se encontram, interferência construtiva ![]()
A diferença de distância é dada por:
d = | PF1 – PF2 |
(O módulo é necessário porque não existe distância negativa.)
A distância também é dada por
Se n for par, temos IC; se n for ímpar, temos ID.
Ondas estacionárias
Quando duas ondas idênticas (de mesma frequência, mesma amplitude e mesmo comprimento de onda) se propagam na mesma direção, mas seguem percursos em sentido oposto, cria-se um tipo de interferência chamada ondas estacionárias. Nesse tipo de interferência, os pontos máximo e mínimo (crista e vale) se mantêm fixos ao longo do percurso entre a fonte e o ponto em que a onda se reflete de volta. É o que ocorre com as ondas emitidas pelas cordas de um instrumento musical – um violão ou violino, por exemplo. Cada uma das cordas mantém um padrão estacionário entre o ponto em que é emitida.
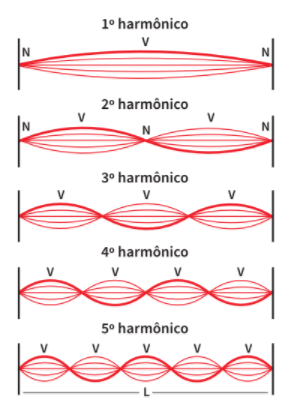
Quando um violonista toca, o som emitido pelo instrumento é resultado da vibração das cordas, que emitem ondas de diferentes frequências, criando diferentes harmônicos, ou modos de vibração. Um harmônico se caracteriza pelo número de ventres (V) – regiões em que as cordas vibram em interferência construtiva. Os ventres são separados por nós (N), pontos em que a vibração das cordas produz uma interferência destrutiva. Veja na figura abaixo.
Veja que:
• o 1o harmônico tem dois nós (N) e um único ventre (V). O comprimento de onda é igual ao comprimento da corda (L);
• o 2o harmônico tem dois V, que têm metade do comprimento de L. O comprimento dessa onda, portanto, é metade do comprimento da onda no 1o harmônico.
E assim por diante.
A relação geral entre o comprimento de onda dos harmônicos é dada por:
Em que n é a ordem do harmônico.
Pela equação fundamental da ondulatória, obtemos a frequência do enésimo harmônico:
Quanto maior a frequência de uma onda sonora, mais agudo é o som obtido. Um som com uma frequência duas vezes maior que outro está uma oitava acima na escala musical.
Efeito Doppler
É a variação aparente de uma onda emitida por uma fonte F para um observador, causada pelo movimento da fonte em relação a esse observador. É esse efeito que faz com que, numa corrida de Fórmula 1, o som do motor dos carros pareça cada vez mais agudo, conforme se aproxima e, depois, cada vez mais grave, à medida que se afasta. A frequência do som nunca se altera. É o movimento da fonte em relação ao observador que gera essa sensação.
Se a fonte se aproxima observador, o valor da frequência aparente é maior que a frequência real (Fap > Freal). Caso a fonte se afaste do observador, o valor da frequência aparente é menor que da frequência real (Fap < Freal).
O efeito Doppler ocorre também com ondas eletromagnéticas, como a luz. A astronomia utiliza esse efeito para descobrir se um corpo distante no Cosmo se afasta ou se aproxima de nós. Quando uma galáxia se afasta, sua luz tende para o vermelho – a cor cujas ondas têm a menor frequência no espectro magnético visível. Quando se aproxima, a cor tende para o azul, cor de frequência maior.
Os radares nas estradas também empregam o efeito Doppler para medir a velocidade de um carro. O radar emite ondas eletromagnéticas de uma frequência conhecida F0 e capta as ondas refletidas no veículo, com uma frequência aparente, Fap. Se o carro se aproxima do radar, Fap é menor que F0; caso se afaste, Fap é maior que F0. A diferença entre F0 e Fap define a velocidade do veículo.
Considerando que uma fonte se movimenta com velocidade Vf, emitindo ondas que se propagam com velocidade V, e um observador que se desloca com velocidade Vo, o valor da frequência aparente (Fap) é dada por:
Repare que a fórmula traz o sinal ± tanto no numerador quanto no denominador. Isso porque o resultado da expressão depende do referencial adotado para o movimento e do sentido em que esse movimento ocorre. Ou seja, para calcular a frequência aparente é preciso adotar um referencial. E a orientação deve ser sempre do observador para a fonte.
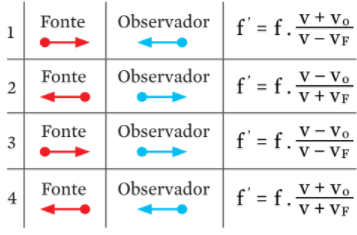
Veja como os sinais para as velocidades do observador (Vo) e da fonte (Vf) variam conforme o movimento relativo entre o observador e a fonte.
Repare:
• Se o movimento se dá em sentidos contrários (1 e 2), os sinais de Vo e Vf também são contrários, dependendo do sentido em que cada um segue (se afastam ou se aproximam).
• Se o movimento se dá no mesmo sentido (3 e 4), Vo e Vf têm o mesmo sinal: negativo se o observador segue na frente; negativo, se ele segue atrás.

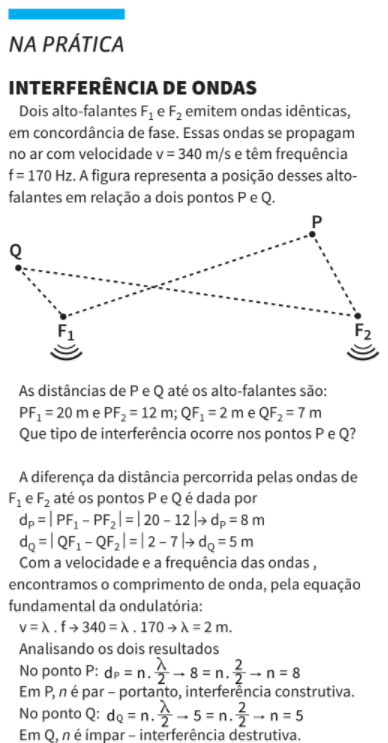
NA PRÁTICA: FREQUÊNCIA APARENTE
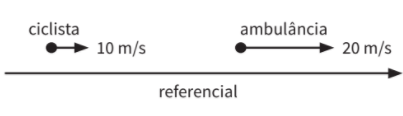
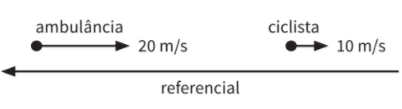
Por uma rua circulam, no mesmo sentido, um ciclista e uma ambulância. O ciclista pedala a 10 m/s e a ambulância se desloca a 20 m/s. Considere que a velocidade do som no ar seja de 340 m/s e que a frequência real do som emitido pela ambulância seja de 720 Hz. Qual é a frequência aparente do som da sirene quando
a) o ciclista segue atrás da ambulância?
b) a ambulância segue atrás do ciclista?
c) Indique se o som fica mais agudo ou mais grave, em cada uma das situações.
Resolvendo as questões:
a) O ciclista e a ambulância deslocam-se no mesmo sentido, com a ambulância (fonte) à frente:
Observador e fonte seguem no mesmo sentido, com a fonte à frente. Como o referencial é sempre o ciclista (observador) as velocidades são todas positivas:
Pela expressão que dá a frequência aparente, temos:
b) A ambulância segue atrás do ciclista:
O ciclista é o referencial do movimento. Então, as velocidades têm o mesmo sinal, mas negativo:
Vobs = – 10 m/s e Vf= – 20 m/s. Pela expressão que dá a frequência aparente, temos:
c) No primeiro caso (ciclista atrás da ambulância), a frequência aparente é menor que a frequência real. O som, portanto, é mais agudo. No segundo caso (ambulância atrás do ciclista), a frequência é maior que a real – som mais grave.