Potenciação

A ESCALA DA NANOTECNOLOGIA. Potências de dez com expoente negativo são ideais para indicar o tamanho de robôs minúsculos como estes, entre hemácias.
A POTÊNCIA DE UM NÚMERO
A operação de potenciação nada mais é que o número multiplicado por ele mesmo seguidas vezes.
A medida da magnitude de um terremoto é dada pela escala Richter, baseada em funções logarítmicas. Para entender bem como funcionam os logaritmos, vamos antes ver as operações com potências. Potenciação nada mais é que a multiplicação de um número por ele mesmo, por várias vezes:
22 = 2 . 2 = 4
23 = 2 . 2 . 2 = 8
Uma potência é sempre indicada na forma ab = c, com a ≠ 0, em que a é a base; b é o expoente; c é a potência.
Potências de base 10
As potências de base 10 são especialmente úteis para facilitar os cálculos e estabelecer ordens de grandeza, na notação científica (veja o quadro Saiba mais, ao lado). Veja como é simples escrever um número com muitos zeros usando potência de base 10. Por exemplo:

Pelo número de zeros, percebemos que esse va- lor é resultado da multiplicação de 15 por 10 vezes o número 10. Então 150 000 000 000 = 15 . 1010.
Repare que o número de zeros é exatamente o expoente da potência de 10.
Outro exemplo:
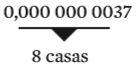
Para escrever esse número usando potência de dez, deslocamos a vírgula no sentido inverso, da esquerda para a direita. O expoente é exatamente o número de casas em que a vírgula foi deslocada. Mas, agora, o expoente é negativo:
0,000 000 0037 = 37 . 10–10
OPERAÇÕES COM POTÊNCIAS
As potências têm propriedades, que definem algumas regras para operar com elas.
- Soma ou subtração de potências: Duas potências só podem ser somadas ou subtraídas se tiverem a mesma base e o mesmo expoente. Veja:
3 . 106 + 4 . 106 = (3 + 4) . 106 = 7 . 106
Repare que somamos apenas as mantissas. A potência fica inalterada. - Já para a soma 7 . 10-5 + 3 . 10-3, a base é a mesma, mas os expoentes são distintos. Para fazer a soma, temos de dar às potências uma mesma ordem de grandeza (mesmo expoente).Vamos passar 3 . 10-3 para a ordem de grandeza -5. Para isso, deslocamos a vírgula duas casas para a direita: 3 . 10-3 = 300 . 10-5.
Agora a soma é possível:
7 . 10-5 + 300 . 10-5 = 307 . 10-5. - Produto de potências de mesma base: Ao multiplicar potências de mesma base, somamos os expoentes: am . an = a (m + n)
Exemplo: 26 . 25 = 2 (6 + 5) = 211. - Quociente de potências de mesma base: Na divisão de potências de mesma base, subtraímos um expoente de outro:
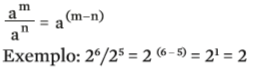
- Potência de potência: Os expoentes são multiplicados: (am)n = am . n.
Exemplo: (32)2 = (3 . 3)2 = 92 = 9 . 9 = 81.
Pela propriedade de potência de potência, chegamos mais rapidamente ao resultado:
(32)2 = 3(2 . 2) = 34 = 3 . 3 . 3 . 3 = 81 - Potência de expoente fracionário: São as potências em que o expoente é uma fração. Nesse caso, a potência indica uma raiz:
Exemplo:
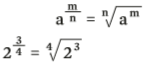
- Potência de um produto: A multiplicação elevada a determinado expoente é igual à multiplicação de cada fator elevado àquele mesmo expoente: (a . b)m = am . bm
Exemplo:
(2 . 3)2 = 22 . 32
(2 . 3)2 = 62 = 36
22 . 32 = 4 . 9 = 36 - Potência de um quociente: Da mesma maneira, uma divisão (ou fração) elevada a deter- minado expoente é igual à divisão de cada fator elevado ao mesmo expoente:
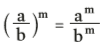
Exemplo:
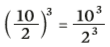
Confira, de novo:
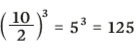
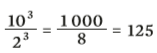

EXPOENTES 1 E ZERO
Um número a elevado a 1 é igual a ele mesmo.
Um número a elevado a 0 é igual a 1, desde que a ≠ 0.

EXPOENTES POSITIVOS E NEGATIVOS
Numa potência de expoente positivo, o número é multiplicado:
52 = 5 . 5 = 25
Já o expoente negativo indica que a base é o denominador de uma fração de numerador 1:
![]()
Como regra geral, lembre-se que:
![]()

NOTAÇÃO CIENTÍFICA
Notação científica é a forma como a ciência apresenta valores. Um número está em notação científica quando aparece na forma n = k . 10x, em que 1 ⩽ k < 10.
Isso significa que k (chamado mantissa) é sempre um valor entre 1 e 9,9999999…. (indefinidas casas decimais) – jamais menor que 1 e nunca igual a 10 ou superior a isso.
Alguns exemplos de transformação de um número em notação científica:
- 15 . 1010, em notação científica, é escrito como 1,5 . 1011
- 37 . 10–8, em notação científica, é expresso como 3,7 . 10–9
Números assim pequenos são usados, por exemplo, para as dimensões diminutas da nanotecnologia, área da engenharia que lida com objetos do tamanho de moléculas .











