Um mês para o Enem: os 5 assuntos de Matemática que você precisa revisar
Os temas campeões nesse ranking são Matemática Básica, Estatística, Geometrias Espacial e Plana, e Funções

Como estão seus estudos para o Enem? Falta exatamente um mês para a prova e a lista de conteúdos é gigante. Por isso, é preciso tomar muito cuidado para não se perder, principalmente quando se fala em Matemática – uma das disciplinas mais desafiadoras para a maioria dos estudantes.
Uma boa dica para esta reta final dos estudos é se concentrar nos temas que mais caem na prova. Mas, afinal, quais são? Para sanar essa dúvida, o cursinho Aprova Total! desenvolve todos os anos a sua Análise de Incidências Enem, que estuda as últimas edições da prova, pergunta por pergunta. As questões são divididas por temas e, assim, chega-se à conclusão dos assuntos mais pedidos.
Top 5 de Matemática
Segundo o levantamento, Matemática Básica está em primeiro lugar, com 33,8%. Em seguida, vem Estatística, com 12,5%. As duas juntas somam quase metade das questões! Elas são seguidas de Geometria Espacial (11,4%), Funções (10,8%) e Geometria Plana (8%).
Abaixo, Jessica Rama, autora de Matemática do Sistema de Ensino pH, explica o que é cada um desses cinco assuntos, com exemplos de questões do Enem. Vem com a gente!
1. Matemática Básica
Como o próprio nome sugere, é o básico da matemática que qualquer estudante precisa saber ao finalizar o Ensino Médio. Nessas questões, são avaliados o raciocínio lógico, a interpretação de problemas e a capacidade de resolver questões contextualizadas do dia a dia. Entre os conteúdos mais cobrados de Matemática Básica estão:
- operações básicas (soma, subtração, divisão, multiplicação);
- múltiplos e divisores;
- notação científica;
- Sistema de Numeração e Métrico Decimal;
- unidades de medida de massa, capacidade e volume;
- porcentagem;
- razão e proporção.
Ah, uma última dica: saber usar a regra de 3 pode te salvar em todos estes tópicos!
Exemplo de questão do Enem 2020
Um grupo sanguíneo, ou tipo sanguíneo, baseia-se na presença ou ausência de dois antígenos, A e B, na superfície das células vermelhas do sangue. Como dois antígenos estão envolvidos, os quatro tipos sanguíneos distintos são:
- Tipo A: apenas o antígeno A está presente;
- Tipo B: apenas o antígeno B está presente;
- Tipo AB: ambos os antígenos estão presentes;
- Tipo O: nenhum dos antígenos está presente.
Foram coletadas amostras de sangue de 200 pessoas e, após análise laboratorial, foi identificado que em 100 amostras está presente o antígeno A, em 110 amostras há presença do antígeno B e em 20 amostras nenhum dos antígenos está presente.
Dessas pessoas que foram submetidas à coleta de sangue, o número das que possuem o tipo sanguíneo A é igual a:
a) 30.
b) 60.
c) 70.
d) 90.
e) 100.
Resposta pelo Anglo Resolve:
Denotando por A o conjunto das amostras de sangue que possuem o antígeno A, B o conjunto das amostras de sangue que possuem o antígeno B e x a quantidade de amostras que possuem os dois antígenos, do enunciado, podemos construir o seguinte diagrama:
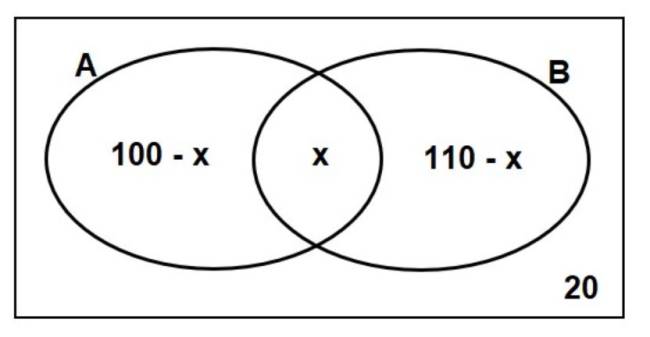
Como o total de amostras é 200, devemos ter:
(110 – x) + x + (100 – x) + 20 = 200 → x=30
Logo, o número de amostras que possuem somente o antígeno A é dado por:
100 – x = 100 – 30 = 70.
Alternativa correta é letra C.
2. Estatística
As questões de Estatística no Enem são sobre coletar, organizar e interpretar dados para tirar conclusões. O foco aqui é entender as informações numéricas que aparecem em gráficos e tabelas, e tomar decisões com base nelas. A boa notícia? Não precisa se preocupar com cálculos complexos. Ufa! O que mais cai:
- média, mediana, moda;
- variância e desvio padrão (noções básicas);
- probabilidade: eventos simples e compostos;
- interpretação de gráficos e tabelas.
Exemplo de questão do Enem 2019
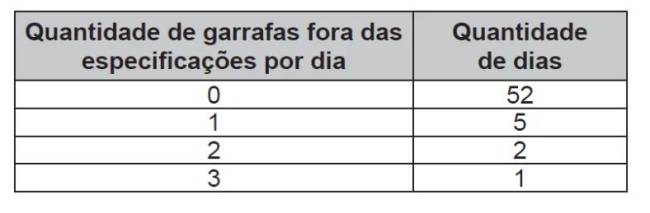
Em uma fábrica de refrigerantes, é necessário que se faça periodicamente o controle no processo de engarrafamento para evitar que sejam envasadas garrafas fora da especificação do volume escrito no rótulo. Diariamente, durante 60 dias, foram anotadas as quantidades de garrafas fora dessas especificações. O resultado está apresentado no quadro.
Para facilitar a análise sobre a quantidade de gols marcados por esses artilheiros nas referidas copas, foi calculada a mediana da distribuição dos números de gols marcados por eles nas sete copas especificadas no quadro.
A média diária de garrafas fora das especificações no período considerado é:
a) 0,1
b) 0,2
c) 1,5
d) 2,0
e) 3,0
Resposta pelo Anglo Resolve:
A média é dada por:
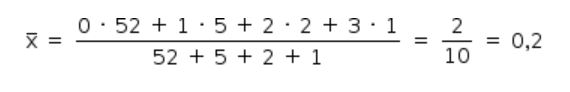
Alternativa correta é letra B.
3. Geometria espacial
Geometria espacial é o estudo e a análise de objetos que ocupam espaço, ou seja, aqueles que têm três dimensões: altura, largura e profundidade. No Enem, você vai precisar saber como calcular volumes, áreas de superfícies, e entender como esses sólidos geométricos aparecem no nosso dia a dia. Um exemplo é como calcular o volume de uma caixa ou entender como a forma de um objeto afeta seu uso. As figuras mais pedidas são:
- prismas;
- pirâmides;
- cilindros;
- cones;
- troncos (cone e pirâmide);
- esferas;
- projeções ortogonais.
Exemplo de questão do Enem 2021
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.

Sabe-se que 1 cm3 = 1 ml e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
a) 216
b) 408
c) 732
d) 2196
e) 2928
Resposta pelo Anglo Resolve:
Considere a figura a seguir, em que foram construídos dois cones semelhantes entre si a partir do tronco que corresponde ao formato da caneca.

Da figura, tem-se:

Assim, o cone maior possui altura igual a x + 12, ou seja, 60 cm, e raio da base de medida 5 cm.
Já a altura do cone menor é x, ou seja, 48 cm, e seu raio da base mede 4 cm.
Logo, o volume “V” da caneca, em cm3, é dado pela diferença entre o volume do cone maior e o volume do cone menor:

Como 1 cm3 = 1 mL, a capacidade volumétrica da caneca é de 732 mL.
Com isso, alternativa correta é letra C.
4. Funções
São expressões que representam a relação entre dois conjuntos numéricos e que podem ser apresentadas por gráficos. No Enem, o papo é prático: geralmente envolve situações como crescimento populacional, variação de preços e até o movimento de objetos. Ou seja, funções têm tudo a ver com usar matemática para entender e resolver situações reais, de um jeito bem aplicado. O que mais cai na prova:
- funções do primeiro e segundo grau;
- funções exponenciais e logarítmicas (conceitos básicos);
- análise e interpretação de gráficos de funções.
Exemplo de questão do Enem 2021
Uma pessoa pretende viajar por uma companhia aérea que despacha gratuitamente uma mala com até 10 kg.
Em duas viagens que realizou, essa pessoa utilizou a mesma mala e conseguiu 10 kg com as seguintes combinações de itens:

Qual a quantidade máxima de camisetas que essa pessoa poderá levar?Para ter certeza de que sua bagagem terá massa de 10 kg, ela decide levar essa mala com duas calças, um sapato e o máximo de camisetas, admitindo que itens do mesmo tipo têm a mesma massa.
a) 22
b)24
c) 26
d) 33
e) 39
Resposta pelo Anglo Resolve:
A partir dos dados da tabela, multiplicando a linha da viagem II por 2 e subtraindo a linha da viagem I, tem-se que 2·18 – 12 = 24 camisetas, 2·3 – 4 = 2 calças e 2·2 – 3 = 1 sapato, juntos, terão massa 2·10 – 10 = 10 kg.
Assim, o máximo de camisetas que essa pessoa poderá levar será 24, alternativa B.
5. Geometria plana
É o estudo das formas geométricas que possuem apenas duas dimensões (largura e altura), como quadrado, triângulo, retângulo etc. No Enem, você vai ver muita coisa do dia a dia, como calcular o perímetro de um terreno, a área de um quarto, ou até analisar ângulos e propriedades dessas figuras. É sobre entender as formas à sua volta e resolver problemas práticos de um jeito simples e eficiente. Olha só as figuras planas que mais aparecem nas provas:
- ângulos e retas;
- círculo e circunferência;
- área de figuras planas;
- polígonos e polígonos regulares;
- quadriláteros notáveis;
- relações métricas no triângulo retângulo;
- semelhança de triângulos.
+ A importância do teorema de Pitágoras e da matemática, além das provas
Exemplo de questão do Enem 2017 (segunda aplicação)
Um fabricante recomenda que, para cada m² do ambiente a ser climatizado,são necessário 800 BTUh desde que haja até duas pessoas no ambiente. A esse número devem ser acrescentados 600 BTUh para cada pessoa a mais, e também para cada aparelho eletrônico emissor de calor no ambiente. A seguir encontram-se as cinco opções de aparelhos desse fabricante e suas respectivas capacidades térmicas:
- Tipo I: 10 500 BTUh
- Tipo II: 11 000 BTUh
- Tipo III: 11 500 BTUh
- Tipo IV: 12 000 BTUh
- Tipo V: 12 500 BTUh
O supervisor de um laboratório precisa comprar um aparelho para climatizar o ambiente. Nele, ficarão duas pessoas mais uma centrífuga que emite calor. O laboratório tem a forma de trapézio retângulo, com as medidas apresentadas na figura.
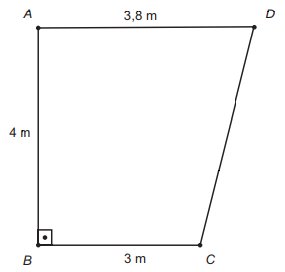
Para economizar energia, o supervisor deverá escolher o aparelho de menor capacidade térmica que atenda às necessidades do laboratório e às recomendações do fabricante.
A escolha do supervisor recairá sobre o aparelho do tipo
a) I
b) II
c) III
d) IV
e) V
A área do trapézio é: (3,8 + 3)4/2 = 13,6 m²
A quantidade mínima de BTUh é 13,6 . 800 + 600 = 11 480.
A escolha será o modelo III, alternativa C.
Cronograma Enem 2024
Inscrições: 27 de maio a 14 de junhoPagamento taxa de inscrição: 27 de maio a 19 de junhoPedido de tratamento pelo nome social: 27 de maio a 14 de junhoSolicitação de atendimento especializado: 27 de maio a 14 de junhoResultado do pedido de atendimento especializado: 17 de junhoRecurso do pedido de atendimento especializado: 17 a 21 de junhoResultado do recurso para atendimento especializado: 27 de junho- Aplicação das provas: 3 e 10 de novembro
- Divulgação do gabarito: 20 de novembro
- Divulgação do resultado: 13 de janeiro




















