Resumo de matemática: Juros simples e compostos
Enquanto o crescimento dos juros simples é linear, o segundo juros compostos é exponencial, e portanto tem um crescimento muito mais acelerado.
Existem dois tipos de juros:
Os juros simples , que são acréscimos somados ao capital inicial no final da aplicação e os juros compostos que são acréscimos somados ao capital, ao fim de cada período de aplicação, formando com esta soma um novo capital, também conhecido como “juros sobre juros”.
Enquanto o crescimento dos juros simples é linear, o segundo juros compostos é exponencial, e portanto tem um crescimento muito mais acelerado.
Como capital definimos o valor que é financiado, seja na compra de produtos ou empréstimos em dinheiro.
Ao financiar algo utilizando juros simples, a pessoa obtem um montante (valor total a pagar) inferior ao que financia por meio de juros compostos.
A fórmula de resolução de juro simples é a seguinte:
j = C. i. t
Na qual:
j = juros, C = capital, i = taxa, t = tempo.
Já a fórmula para juros compostos é:
onde S = montante, P = principal, i = taxa de juros e n = número de períodos que o principal P (capital inicial) foi aplicado.
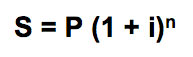

 SEGUIR
SEGUIR
 SEGUINDO
SEGUINDO





















